•Es imposible efectuar análisis químicos totalmente libres de errores o incertidumbres.
•La fiabilidad de un resultado se analiza de diferentes maneras.
•Se analizan patrones de composición conocida.
•Se aplican pruebas estadísticas a los datos.
ERRORES EN LOS ANÁLISIS QUÍMICOS
OBJETIVOS:
· Diseñar un blog y plantear una exposición una exposición power point, sobre un tema de química analítica.
· Conocer la importancia de las tecnologías de la información y comunicación, como un elemento didáctico, para el aprendizaje de las diferentes áreas del conocimiento.
TABLA DE CONTENIDO
1. Mapa Conceptual.
2. Conceptualización.
3. Términos Importantes.
3.1 Media y Mediana.
3.2 Precisión y exactitud.
3.3 Tipos de errores
4. Errores Sistemáticos.
4.1 Fuentes de errores sistemáticos.
4.2 Efectos de los errores sistemáticos.
4.3 Detección de errores sistemáticos.
4.3.1 Instrumentales
4.3.2 De método.
5. Errores aleatorios
5.1 Tratamiento estadístico del error aleatorio:

CUANDO SE APLICA LA ESTADÍSTICA A UN ANÁLISIS
La aplicación de la estadística en todos los pasos de una medida química asegura la calidad de la medición
ADQUISICIÓN DE DATOS
DURANTE
DISEÑO EXPERIMENTAL ANÁLISIS MANIPULACIÓN DE LOS DATOS
ANTES DESPUÉS
UN RESULTADO CONFIABLE ES AQUEL QUE DE MUESTRA
SER VALIDO
validez : Grado al cual una medición
(realizada mediante un instrumento Y/o procedimiento
analítico específicos) produce el resultado esperado
¿ Qué
es estadística?
La
estadística es una colección de métodos para planificar y realizar
experimentos, obtener datos y luego analizar, interpretar, y formular una
conclusión basada en esos datos. Es la ciencia encargada de recopilar,
organizar, analizar e interpretar información numérica o cualitativa, de
manera que pueda llevar a conclusiones válidas.
Estadística en química analítica
Durante la realización de una
análisis cuantitativo es muy importante tomar en cuenta todas las variables que
pueden afectar nuestro resultado, dentro de estos están los factores provocados
por los instrumentos utilizados y los errores provocados por quien maneja el
material.
En
el reporte de cualquier análisis químico, es importante tomar en cuenta este
tipo de errores , hacer un análisis de los resultados y así se podrá concluir
sobre él.
2. Conceptualización
- Coloquialmente, es usual el empleo del término error como análogo o equivalente a equivocación.
- En ciencia e ingeniería, el error, está más bien asociado al concepto de INCERTEZA, INCERTIDUMBRE, en la determinación del resultado de una medición.
SEGÚN SKOOG (2001) EL TERMINO ERROR TIENE DOS SIGNIFICADOS DIFERENTES ENTRE SI:
En primer lugar error se refiere En el segundo lugar el error
como la diferencia entre un suele denotar la incertidumbre
valor medido y el valor verdadero estimada en una medicio o
o conocido. experimento.
como la diferencia entre un suele denotar la incertidumbre
valor medido y el valor verdadero estimada en una medicio o
o conocido. experimento.
- LO MAS COMÚN ES QUE LOS ERRORES SE DERIVAN DE CALIBRACIONES O ESTANDARIZACIONES DIFERENTE, O DE VARIACIONES E INCERTIDUMBRES ALEATORIAS EN LOS RESULTADOS. SOLO ALGUNOS ERRORES SE DEBEN A EQUIVOCACIONES DEL EXPERIMENTADOR.
3. Términos Importantes
3.1. Media y Mediana
Media, Media aritmética y promedio (X) son términos sinónimos. Es la
medida de tendencia central mas utilizada .Se obtiene dividiendo la suma de los
valores de una serie y dividiendo por el numero de medidas del conjunto.
 es el símbolo de la media aritmética.
es el símbolo de la media aritmética.
Ejemplo: Los pesos de seis amigos son: 84, 91, 72, 68, 87 y 78kg. Hallar el peso medio.
Media aritmética para datos agrupados
Ejercicio de media aritmética:
En un test realizado a un grupo de 42 personas se han obtenido las puntuaciones que muestra la tabla. Calcula la puntuación media.
| xi | fi | xi · fi | |
|---|---|---|---|
| [10, 20) | 15 | 1 | 15 |
| [20, 30) | 25 | 8 | 200 |
| [30,40) | 35 | 10 | 350 |
| [40, 50) | 45 | 9 | 405 |
| [50, 60 | 55 | 8 | 440 |
| [60,70) | 65 | 4 | 260 |
| [70, 80) | 75 | 2 | 150 |
| 42 | 1 820 |
Propiedades de la media aritmética
La suma de las desviaciones de todas las puntuaciones de una distribución respecto a la media de la misma igual acero.
 La suma de las desviaciones de los números 8, 3, 5, 12, 10 de su media aritmética 7.6 es igual a 0:
La suma de las desviaciones de los números 8, 3, 5, 12, 10 de su media aritmética 7.6 es igual a 0:
8 − 7.6 + 3 − 7.6 + 5 − 7.6 + 12 − 7.6 + 10 − 7.6 =
= 0. 4 − 4.6 − 2.6 + 4. 4 + 2. 4 = 0
La suma de los cuadrados de las desviaciones de los valores de la variable con respecto a un número cualquiera se hace mínima cuando dicho número coincide con la media aritmética.
4. Si todos los valores de la variable se multiplican por un mismo número la media aritmética queda multiplicada por dicho número.
Mediana
Es el resultado alrededor del
cual se reparten los demás por igual. Si la serie es un numero impar la mediana
es el numero de la mitad. Si la serie es un numero par se toma el promedio del
par central después de haber ordenado la serie de menor a mayor.
3.2. Presición y Exactitud
Presición:
El término precisión describe la reproducibilidad de los resultados y se puede definir como la concordancia que hay entre los valores numéricos de dos o más mediciones que se han realizado de idéntica manera.
La
precisión sólo depende de
la distribución de
los errores aleatorios
y
no se relaciona con
el valor verdadero ni con
el valor especificado.
•Para describir la precisión de un conjunto de datos repetidos se utilizan tres términos muy conocidos: - La desviación estándar
- La varianza
- El coeficiente de variación.
- La varianza: Es la media de los
cuadrados de las diferencias entre cada valor de la variable y la media
aritmética de la distribución. Aunque esta
fórmula es correcta, en la práctica interesa realizar inferencias
poblacionales, por lo que en el denominador en vez de n, se usa n-1
- Coeficiente de variación: C.V = S/Media *100.
Desviación estándar
La desviación estándar (σ) mide cuánto se separan los datos.
La fórmula es fácil: es la raíz cuadrada de la varianza. Así que, "¿qué es la varianza?"
Varianza
la varianza (que es el cuadrado de la desviación estándar: σ2) se define así:
Es la media de las diferencias con la media elevadas al cuadrado.
Ejemplo
Tú y tus amigos habéis medido las alturas de vuestros perros (en milímetros):
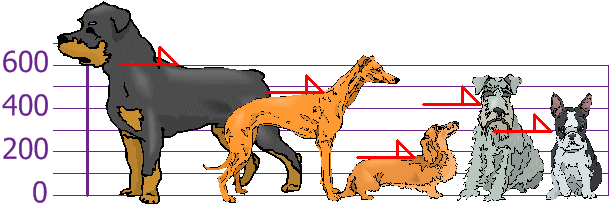
Las alturas (de los hombros) son: 600mm, 470mm, 170mm, 430mm y 300mm.
Calcula la media, la varianza y la desviación estándar.
Respuesta:
| Media = |
600 + 470 + 170 + 430 + 300
| = |
1970
| = 394 |
5
|
5
|
así que la altura media es 394 mm. Vamos a dibujar esto en el gráfico:
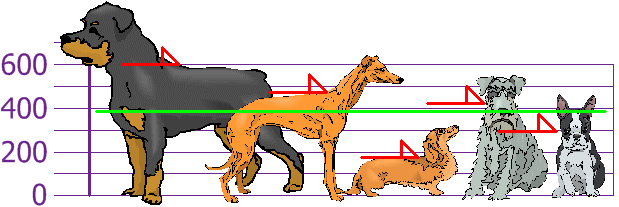
Ahora calculamos la diferencia de cada altura con la media:
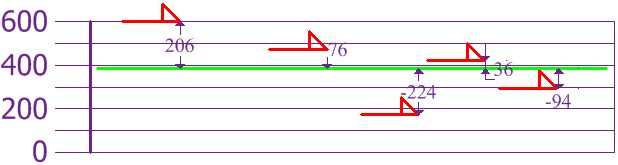
Para calcular la varianza, toma cada diferencia, elevaba al cuadrado, y haz la media:
| Varianza: σ2 = |
2062 + 762 + (-224)2 + 362 + (-94)2
| = |
108,520
| = 21,704 |
5
|
5
|
Así que la varianza es 21,704.
Y la desviación estándar es la raíz de la varianza, así que:
Desviación estándar: σ = √21,704 = 147
y lo bueno de la desviación estándar es que es útil: ahora veremos qué alturas están a distancia menos de la desviación estándar (147mm) de la media:
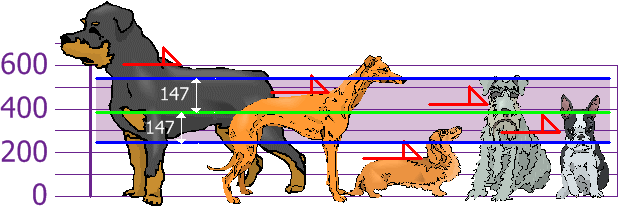
Así que usando la desviación estándar tenemos una manera "estándar" de saber qué es normal, o extra grande o extra pequeño.
*Nota: ¿por qué al cuadrado?
Elevar cada diferencia al cuadrado hace que todos los números sean positivos (para evitar que los números negativos reduzcan la varianza)
Y también hacen que las diferencias grandes se destaquen. Por ejemplo 1002=10,000 es mucho más grande que 502=2,500.
Pero elevarlas al cuadrado hace que la respuesta sea muy grande, así que lo deshacemos (con la raíz cuadrada) y así la desviación estándar es mucho más útil.
Exactitud: Supone una comparación con un
valor verdadero o aceptado como tal, la precisión indica la concordancia entre las
medidas que han sido realizadas de una misma forma.
Esquema
gráfico para comprender la relación entre exactitud y precisión
En
C
existe buena precisión, pero no buena exactitud; en
A
buena exactitud y precisión, y en B
mala exactitud y precisión.
3.3. Tipos de errores:
4. Errores Sistemáticos
4.1 Fuentes de errores sistemáticos:
- Errores instrumentales: Calibraciones deficientes
- Errores del método: Dificiles
de identificar
- Errores personales: Descuido, Falta de atención
4.2 Efectos de los errores sistemáticos
•Los
errores sistemáticos pueden ser constantes o proporcionales.
•En
los errores constantes el error absoluto es invariable con el tamaño de la
muestra ,mientras el error relativo cambia al modificar dicho tamaño.
•Los
errores proporcionales aumentan o disminuyen según el tamaño de la muestra. Con los errores
proporcionales el error absoluto varía con el tamaño de la muestra, en cambio
el error relativo permanece constante.
•En los errores constantes, el error absoluto es invariable con el
tamaño de la muestra, mientras en el error relativo cambia al modificar el
tamaño de la muestra.
•Los errores proporcionales aumentan o disminuyen según el tamaño de la
muestra; con estos errores el error absoluto varía con el tamaño de la muestra
en cambio el error relativo permanece constante.
4.3 Detección de errores sistemáticos.
4.3.1 Instrumentales:
Algunos errores sistemáticos instrumentales se pueden identificar y corregir mediante calibración. la calibración periódica de equipos siempre es aconsejable, ya que la respuesta de muchos instrumentos cambian con el tiempo a raíz del desgaste, corrosión o trato inadecuado.
Algunos errores sistemáticos instrumentales se pueden identificar y corregir mediante calibración. la calibración periódica de equipos siempre es aconsejable, ya que la respuesta de muchos instrumentos cambian con el tiempo a raíz del desgaste, corrosión o trato inadecuado.
4.3.2 De método.
- ANÁLISIS DE MUESTRAS ESTÁNDAR: Materiales de referencia certificados. Contienen uno o mas analitos en concentraciones conocidas.
- ANÁLISIS INDEPENDIENTES: Utilizar un segundo método analítico independiente y seguro. Debe ser lo mas diferente posible.
- DETERMINACIONES BLANCO: Contiene los reactivos y disolventes utilizados. revelan errores debidos a contaminantes.
5. Errores Aleatorios.
•Son la principal fuente de incertidumbre en una determinación.
•Muchas variables no controladas y de no fácil identificación causan errores aleatorios.
•El efecto acumulativo de las incertidumbres, aunque estas sean muy pequeñas, hace que las mediciones por duplicado de una serie fluctúen al azar.
•Los
métodos estadísticos permiten categorizar y caracterizar los datos, y tomar
decisiones objetivas en cuanto a su calidad e interpretación.
•Hay que diferenciar entre muestra y población o universo. ( caso del análisis de Ca en agua. La población seria un numero de medidas muy grande cercano al infinito).
•Las leyes de la estadística se dedujeron para usarlas en poblaciones. Para aplicarlas a muestras se debe hacer ajustes.
•Las curvas gaussianas se pueden representar por medio de una ecuación que tiene la media de la población µ, y la desviación estándar de la población σ.
•Muchas variables no controladas y de no fácil identificación causan errores aleatorios.
•El efecto acumulativo de las incertidumbres, aunque estas sean muy pequeñas, hace que las mediciones por duplicado de una serie fluctúen al azar.
FUENTES
DE LOS ERRORES ALEATORIOS.
Los
errores aleatorios obedecen una curva normal de error o curva de Gauss.
5.1 Tratamiento estadístico del errores aleatorio:
•Hay que diferenciar entre muestra y población o universo. ( caso del análisis de Ca en agua. La población seria un numero de medidas muy grande cercano al infinito).
•Las leyes de la estadística se dedujeron para usarlas en poblaciones. Para aplicarlas a muestras se debe hacer ajustes.
•Las curvas gaussianas se pueden representar por medio de una ecuación que tiene la media de la población µ, y la desviación estándar de la población σ.

REFERENCIAS
*Douglas A. Skoog, Donald M. West-2005. Fundamentos de química analítica







No hay comentarios:
Publicar un comentario